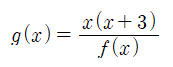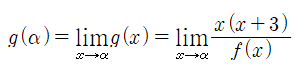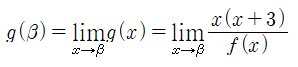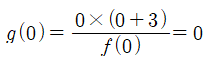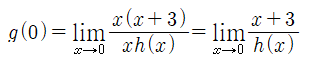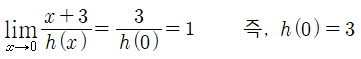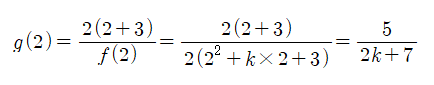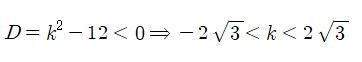먼저, 주어진 (가)에서 g(x)를 어떻게 나타내야 할지 생각해봅시다. f(x)≠0일 때에는 

와 같이 나타낼 수 있을 것입니다. f(x)=0일 때에는 위의 식을 사용할 수 없을텐데요. 만약 f(α)=0인 α에 대하여 g(α)를 구해야 한다면,

와 같이 g(x)가 모든 실수에 대하여 연속임을 이용하여 함숫값 대신 극한값을 구하는 방식을 사용하면 됩니다.

한편, f(x)는 문제조건에서 최고차항의 계수가 1인 삼차함수입니다. 또한, g(x)를 나타내기 위한 위의 분수식을 살펴보면, f(x)=0인 근은 0, -3 이외에는 나와서는 안됨을 알 수 있습니다. 만약 0, -3이 아닌 실수 β에 대하여 f(β)=0이라면,

에서 분모는 0으로 수렴하는데, 분자는 0에 수렴하지 않아, g(β)가 존재하지 않게 됩니다. 즉, g(x)가 모든 실수에 대하여 연속이라는 조건에 위배가 되죠. 이 부분은 나중에 다시 사용되니 주의하고 넘어갑시다.

(가)에서 얻을 만한 것은 충분히 살펴본 것 같으니, 이제 (나)로 가봅시다. (나)에서는 g(0)의 값이 구체적으로 1이라고 주어져 있습니다.  좀 전에 g(x)를 식으로 나타내는 방법을 봤었는데요. g(0)을 구할 때, f(0)≠0라면 제일 처음에 살펴본 식대로

여야 합니다만, (나)에서 g(0)은 0이 아니라 1입니다. 따라서, f(0)=0이고, g(0)은 극한을 통해 구해야 한다는 것을 알 수 있습니다. 즉, f(x)는 x라는 인수를 갖겠군요. f(x)=x·h(x) (h(x)는 최고차항의 계수가 1인 이차함수)라 두고 g(0)을 확인해보겠습니다.

h(0)=0이면 분모만 0으로 수렴하고, 분자는 그렇지 않으므로 g(0)은 수렴하지 않습니다. 즉, h(0)≠0이고, 

따라서 h(x)=x²+kx+3 (k는 상수)라고 둘 수 있겠습니다. f(x)=x(x²+kx+3)이 되겠구요.

이제 문제의 마지막 조건인 f(1)이 자연수임을 사용해봅시다. f의 식은 이미 상당히 구체적으로 구했기때문에 대입만 하면 됩니다. f(1)=1·(1+k+3)=k+4이고, 이 값이 자연수가 되려면, k≥-3, k는 정수임을 쉽게 알 수 있습니다.

그럼 이제 g(2)를 구해봅시다. 앞에서 언급한바와 같이 f(2)≠0이므로,

가 됩니다. 어라.. 위의 식에서 k≥-3, k는 정수만 적용하면 k가 크면 클 수록 g(2)가 작아지는 건데 이상하군요. 뭔가를 빠뜨린 걸까요?

우리는 처음에 f(x)=0은 0, -3 이외의 해를 가진다라고만 했지 이를 만족하기 위한 f(x)의 형태에 대해선 확인해보지 않았죠. 맨 처음 단계에서는 f(x)의 형태를 잡을 수 없는 관계로 그냥 넘어갔습니다만 f(x)=x(x²+kx+3)까지 구한 시점에서는 이를 확인했어야 합니다. f(x)가 이미 x라는 인수를 가지므로 남은 부분인 x²+kx+3는 실근을 0, -3 외에 갖지 않아야 합니다. 상수항이 0이 아니라서 0은 근일 수가 없겠고, -3을 근으로 가지게 되면 근과 계수의 관계에 의해 다른 한 근이 -1이어서 안되겠구요. 결국 아예 실근이 없어야겠군요. 

이므로 가장 큰 k의 값은 3이고, 이때의 g(2)=5/13입니다.

수학의 정도(正道) - 대홍쌤 블로그의 허락을 받아 올리는 해설입니다.