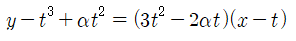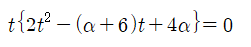문제에서 다항함수 f(x), g(x)에 대한 설명이 간단히 나와있습니다. 내용을 기억하며 바로 (가)로 가봅시다. "어떤 다항함수가 (k, 0)에서 x축에 접하면 (x-k)² 을 인수로 갖는다"라는 사실만 알고 있다면 매우 쉽게 파악할 수 있는 내용입니다. f(x)는 x²을 인수로 가지고 최고차항 계수가 1인 삼차함수이므로 f(x)=x²(x-α)라 둘 수 있고, g(x)는 (x-2)²을 인수로 가지고 최고차항 계수가 -1인 이차함수이므로 g(x)=-(x-2)²입니다. g(x)는 완전히 확정이 되었군요.

(나)에서는 (2,0)에서의 접선의 개수가 2라고 합니다. 전형적인 곡선 y=f(x) 밖의 (또는 밖인지 위인지 알 수 없는) 점에 대한 접선의 방정식을 구하는 방법대로 접점을 (t,f(t))로 두고 풀면 되겠군요. 서로 다른 접선의 개수 = 서로 다른 접점의 개수라는 것을 기억하여 실근 t의 개수를 확인하면 되겠습니다. 

(x, y) = (2, 0)을 대입하여 정리하면,

라는 t의 방정식을 얻을 수 있고, 여기서의 t의 실근은 (2,0)에서 그은 접선에 대한 접점의 x좌표임을 알 수 있습니다. 앞에서 언급한바와 같이 이 방정식의 서로 다른 실근의 개수는 접선의 개수이기도 하기 때문에, 실근의 개수가 2개가 되도록 α를 정해야 합니다.
이미 t=0이라는 실근이 하나 확보가 되어 있으므로 남은 이차방정식 2t²-(α+6)t+4α=0 부분에서는 ① 0과 다른 한 실근을 갖거나, ② 0이 아닌 중근을 가져야 합니다. ①의 경우, t=0을 대입하면 α=0이어야 하고, ②의 경우는 판별식 D=0을 풀면 α=2 or 18입니다.

α=0, 2, 18일 때의 그래프의 개형을 간단히 그려보면 (다)를 만족하는, 즉, f(x)=g(x)의 실근이 하나뿐인 경우는 α=0가 유일함을 알 수 있습니다.

(그래프 추후 추가)

따라서 f(x)=x³으로 결정할 수 있겠습니다.

이제 양수 x에 대하여 g(x)≤kx-2≤f(x)를 만족시키는 k를 찾으면 됩니다. 해당범위에서 이 부등식을 만족시키려면 (0, -2)를 지나고 각각 y=f(x), y=g(x)에 접하는 접선을 그어보면 됩니다.(자세한 설명 추후 추가)
y=f(x)에 접하는 경우의 k=3, y=g(x)에 접하는 경우의 k=4-2root2 이므로 α-β=1+2root2, a²+b² = 5입니다. 

수학의 정도(正道) - 대홍쌤 블로그의 허락을 받아 올리는 해설입니다.