2018년도 수능 수리영역 가형 29번 [진산서당]
지난 2017년 11월 23일(목) 실시된 2018학년도 대학수능 수학 가형 29번 기출문제의 풀이 및 해설입니다.
오답률 2위 94.1%
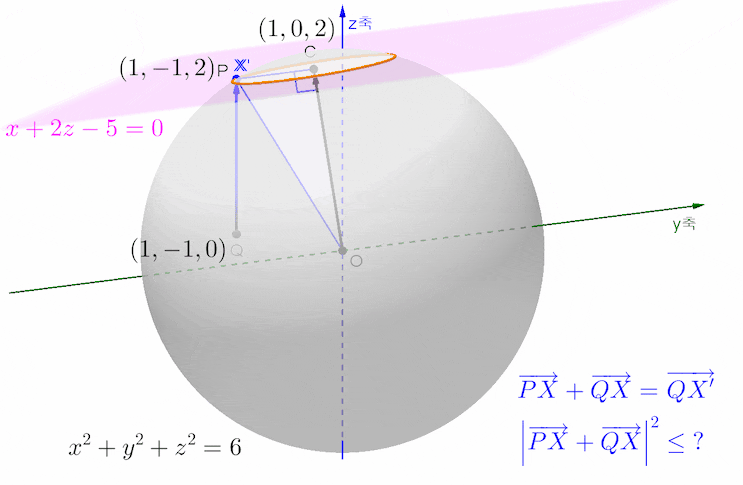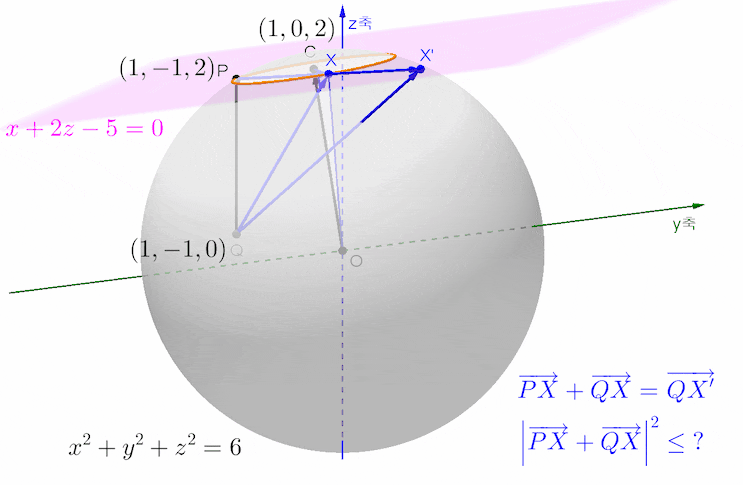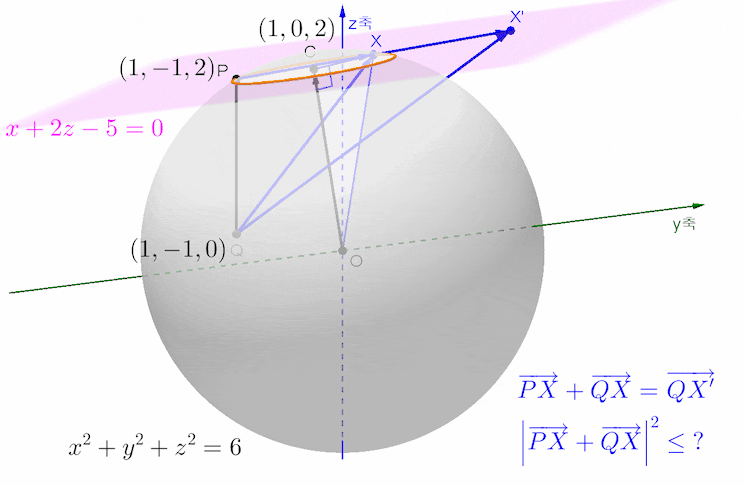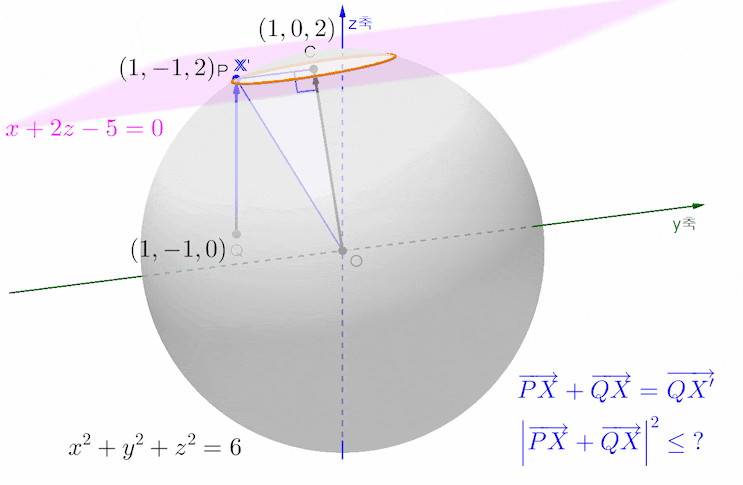
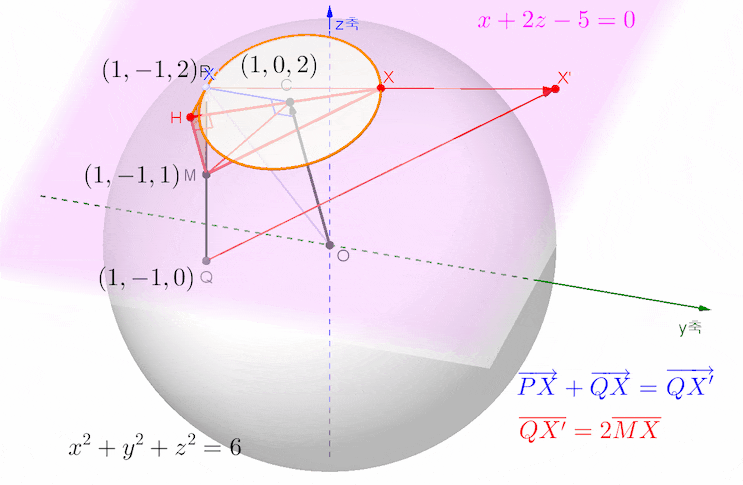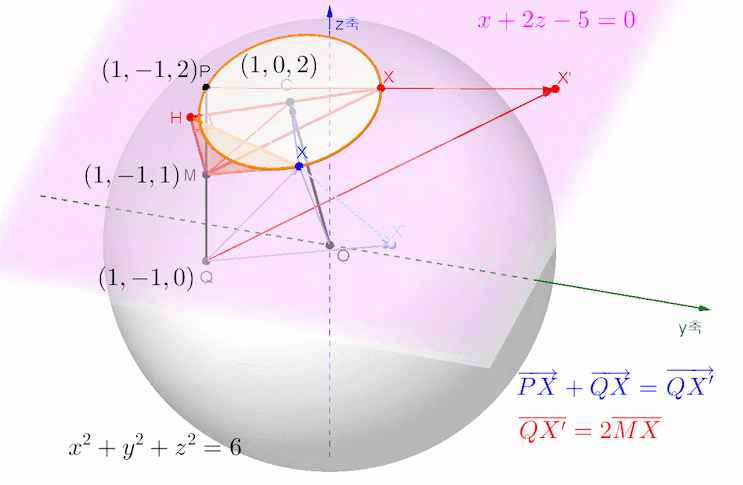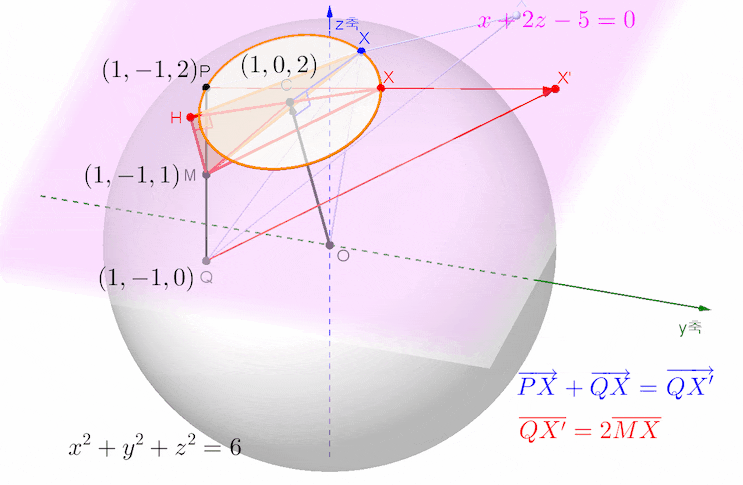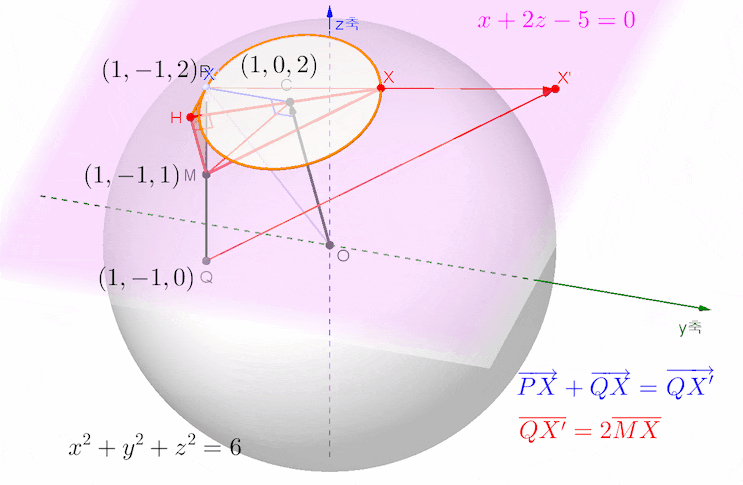
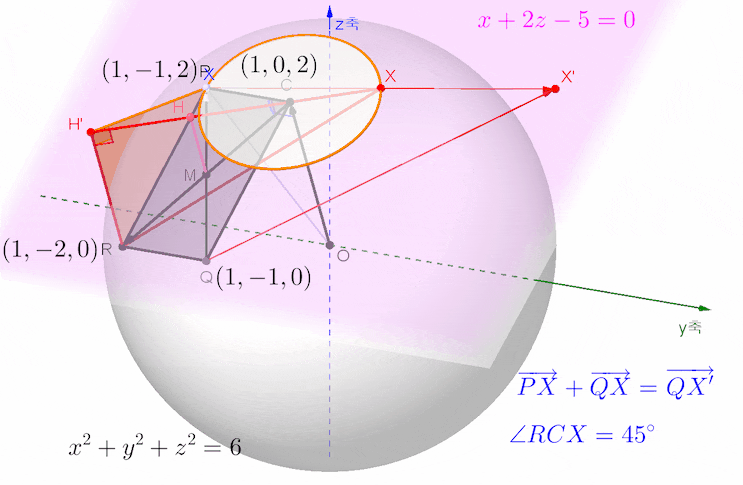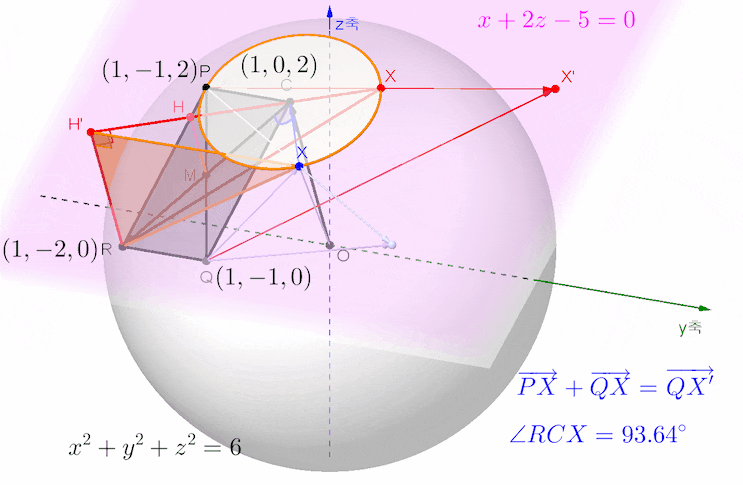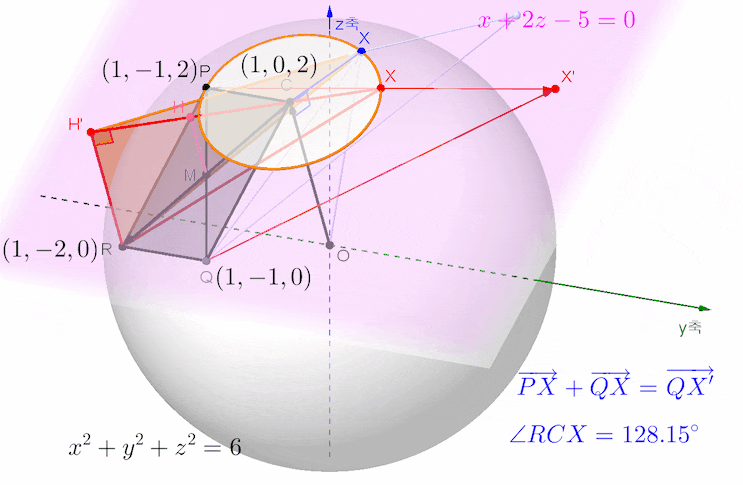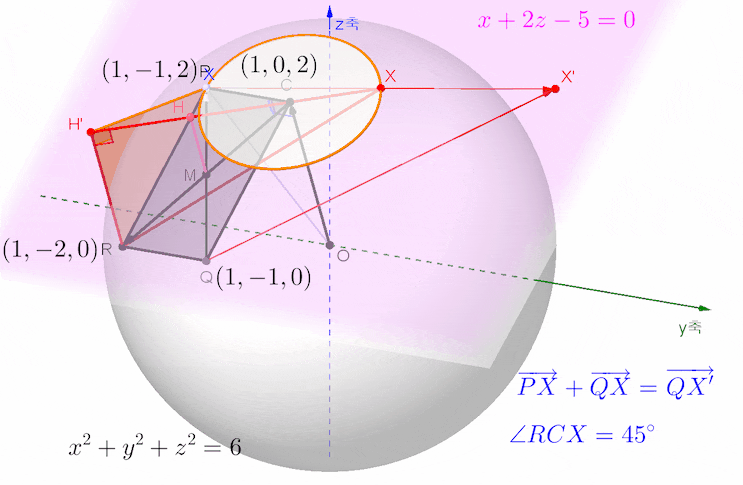
아래 애니메이션은 문제의 뜻을 살펴 보기 위한 목적으로 그려본 것입니다.
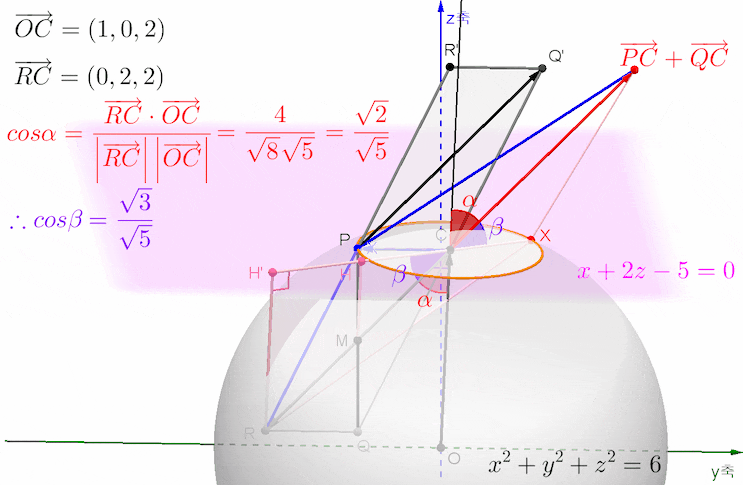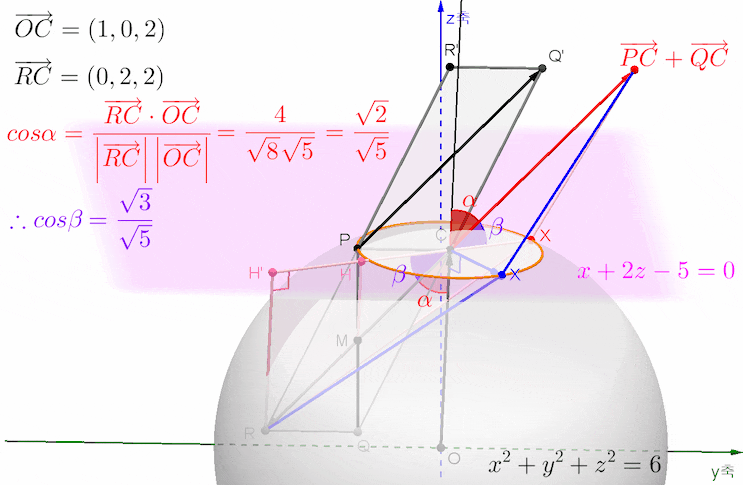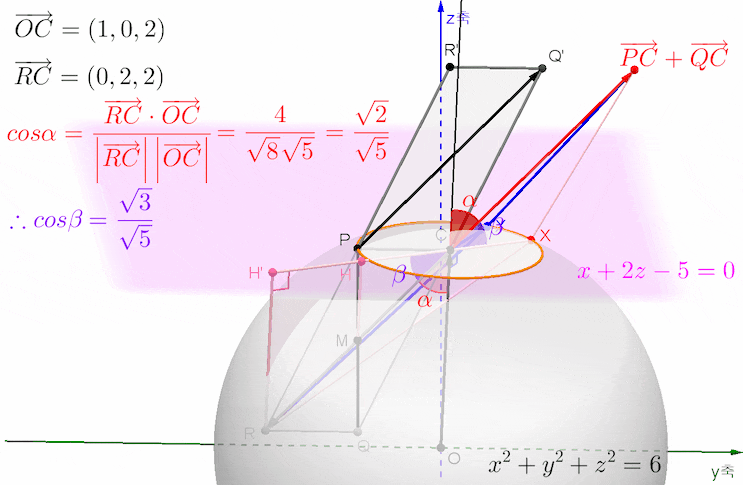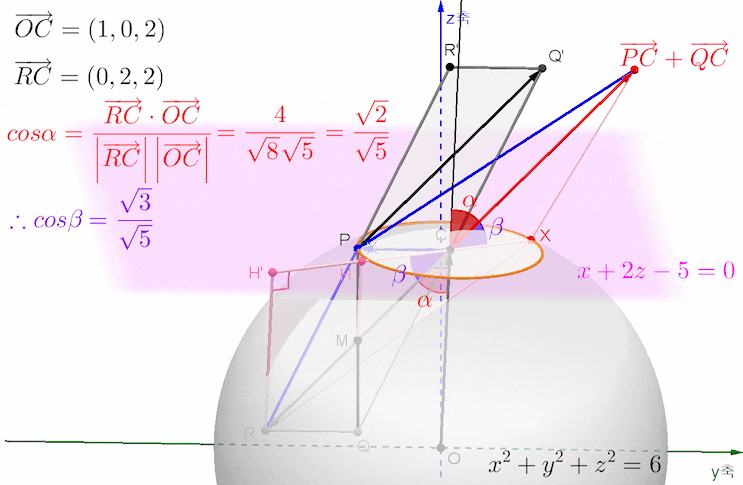
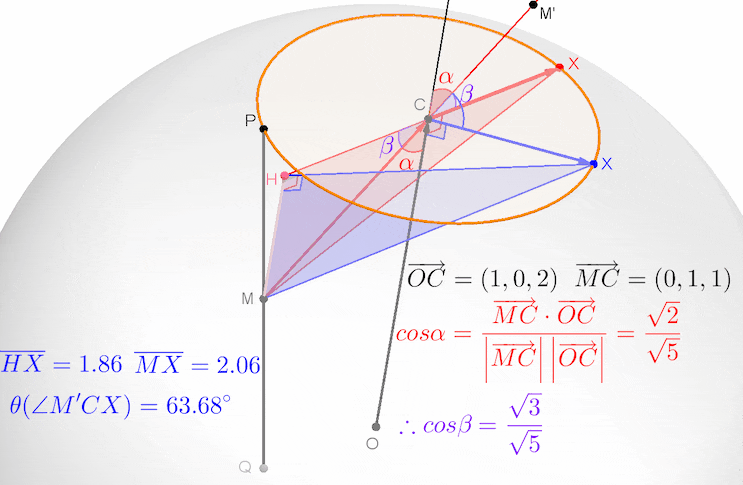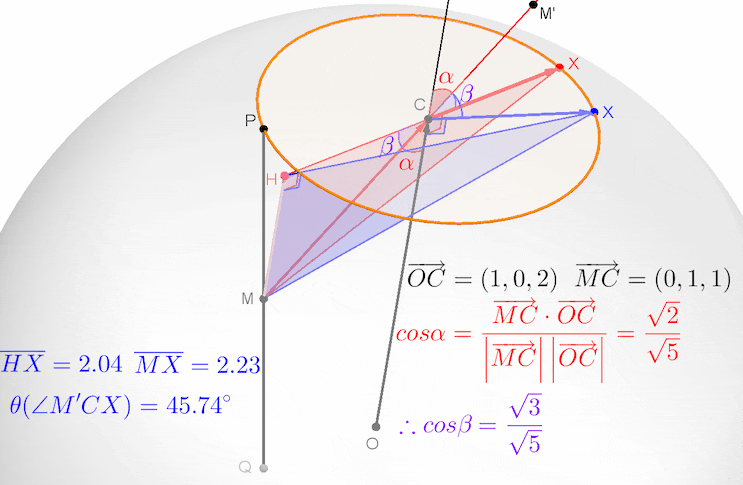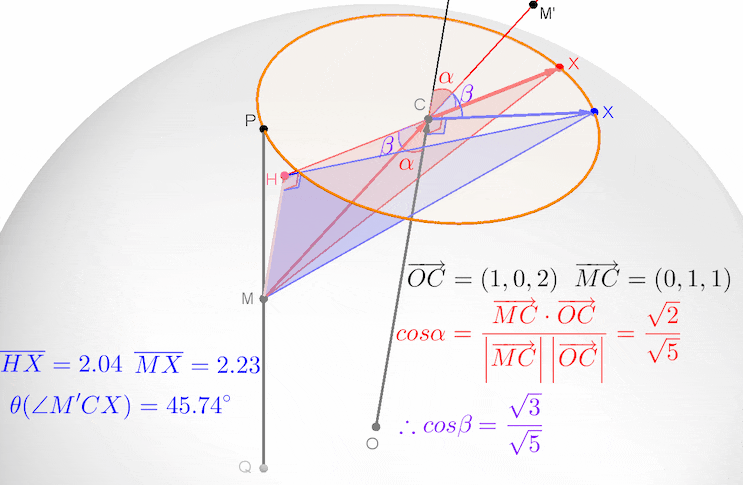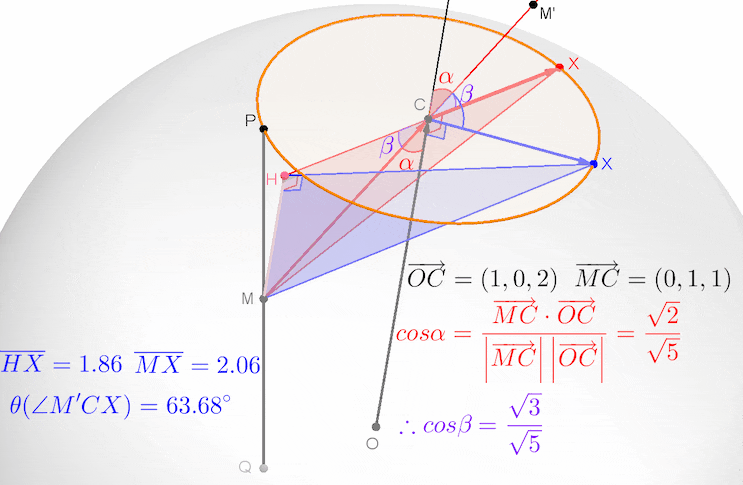
그림에 있는 점 C, P, Q의 좌푯값은 아래와 같이 구한 것입니다.
평면의 법선벡터가 (1, 0, 2)인데, 평면의 방정식에 대입해보니 성립하네요... 이는 점 (1, 0, 2)가 단면원 C의 중심임을 뜻합니다. 일반적으로는 단면원의 중심을 C(t, 0, 2t)로 두고, 평면의 방정식에 대입해서 중심 C의 좌표를 구합니다.
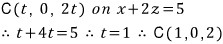
그렇다면, 구의 중심 O에서 단면원 C의 중심 C까지의 거리인 선분 OC의 길이가 √5이고, 구의 반지름의 길이가 √6이므로 단면원 C의 반지름의 길이는 1이 됩니다.
다음,
주어진 평면이 임의의 y 에 대해서 성립하므로 y 축에 평행합니다. 따라서 점 P의 좌표는 (1, -1, 2)이고, 점 Q의 좌표는 (1, -1, 0)이 됩니다.
첫 번째 풀이입니다.
벡터 PX와 QX의 합벡터를 위 그림에서처럼 벡터 QX'로 두고, 원 위를 움직이는 동점 X가 항상 선분 PX'의 중점임을 생각하여 중점연결정리를 떠올렸다면,,,
고정된 수선 PQ의 중점 M을 잡으면 선분 QX'의 길이는 선분 MX의 길이의 두 배가 되므로 선분 MX의 길이가 최대가 되는 상황에 집중하면 될 것입니다.
삼각형 MPX에서 변 MX의 길이는 변 MP가 고정이므로 변 PX의 길이가 길수록, 각 MPX의 크기가 클수록 최대가 됩니다.
이 상황을 찾아내기 위해서는 점 M에서 점 P, X가 놓인 평면에 수선을 내려야겠습니다.
수선의 발을 H라 하면 삼각형 MHX는 각 H가 90°인 직각삼각형이므로 빗변 MX의 길이는 변 HX의 길이가 가장 길 때 최대가 됩니다. 그리고 변 HX의 길이는 원의 중심을 지나는 직선 HC가 원과 만나는 두 점 중에서 점 H에서 멀리 떨어져 있는 교점에 동점 X가 놓일 때 가장 길지요...
먼저,
선분 MH의 길이는 수선 PQ의 중점 M(1, -1, 1)에서 평면 x + 2z - 5 = 0 사이의 거리 공식으로 얻고, 선분 HC의 길이를 직각삼각형 MHC에서 피타고라스의 정리로 구하면 아래와 같이 변 HX의 최댓값을 얻을 수 있으므로
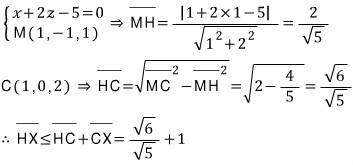
중점을 연결한 선분 MX의 제곱의 최댓값은 아래와 같습니다.
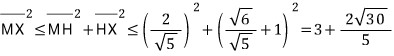
마무리하면,
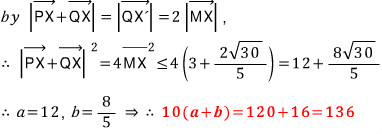
이 풀이에서 선분 HX의 최댓값을 직각삼각형 MHC로부터 얻었습니다만, 수선의 발 H의 좌푯값을 먼저 구하는 방향으로 접근할 수도 있겠습니다.
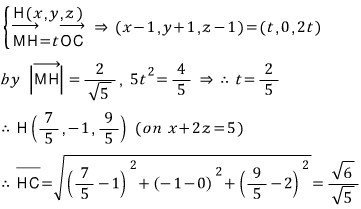
다른 풀이를 생각해 봅니다.
앞 풀이에서는 벡터 PX와 QX의 합벡터의 크기가 최소가 되는 상황을 찾기 위하여 두 벡터의 합벡터를 벡터 QX'로 두고, 중점연결정리를 떠올려서 해결하였습니다만, 이 발상(發想)이 사실은 만만한 것이 아니지요...
보통의 경우 합벡터의 시점이 같은 점일 때가 일반적인데, 이 문제의 경우는 다름으로 인해서 조금 불편합니다. 해서 위의 그림과 같이 처리하는 것은 자연스러우나, 그 다음에 중점연결정리로 나아 가는 발상은 그렇지가 못하지요...
어쨌든
위 그림의 삼각형 QXX'에서 변 QX'의 길이는 변 QX와 XX'의 길이가 길수록, 또 각 QXX'의 크기가 클수록 최대가 됩니다. 그렇다면 벡터 PX와 QX의 크기가 클수록, 외각인 각 PXQ의 크기가 작을수록 변 QX'의 길이가 최대가 되므로, 결국 벡터 XP와 XQ의 내적이 클수록 벡터 PX와 QX의 합벡터의 크기가 커집니다.
원의 중심 C를 기준으로 두 벡터 XP와 XQ를 아래와 같이 분해하여 내적해 보면,
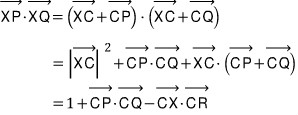
에서
벡터 XC의 크기는 항상 1이고 벡터 CP와 CQ의 내적 및 합벡터 CR가 고정이므로 결국 벡터 CX와 합벡터 CR가 이루는 각이 클수록 내적이 최대가 됩니다.
이상에서,
벡터 CP와 CQ의 합벡터 CR과 벡터 CX가 이루는 각이 클수록 문제의 벡터 PX와 PQ의 합벡터의 크기는 최대가 됩니다.
그리고
벡터 OC가 단면원 C가 놓인 평면의 법선벡터임을 생각하면, 점 R에서 이 평면에 내린 수선의 발을 H'라 하면 직선 H'C는 삼각형 OCR이 놓인 평면과 단면원 C가 놓인 평면의 교선임과 동시에 이 교선이 단면원 C와 만나는 두 점 중에서 H'에서 멀리 떨어져 있는 교점에 동점 X가 놓일 때 합벡터 CR과 벡터 CX가 이루는 각 RCX는 그 크기가 최대가 됩니다.
각 RCX의 크기가 최대인 까닭 보충...
삼각형 RCX에서 변 RC와 CX의 길이가 일정하므로 대변 RX의 길이가 길수록 각 RCX의 크기는 커지는데, 주황색 직각삼각형 RH'X에서 변 RH'의 길이가 일정하고 변 H'X의 길이는 원의 중심 C를 지날 때 최대가 되므로 이때 빗변 RX의 길이가 가장 길게 되지요...
이 부분은 공간벡터 기출에서 자주 등장하는 도형 관계인데요... 특히 단면원과 관련된 문제에서는 단면원이 놓인 평면에 수선을 내림으로써 비로소 이 관계가 보이기 시작한다는 점... 꼭 유념하셔야 겠구요.
아래 게시글들을 함께 참조하십시오.
[수능29번] 2016학년도 대학수능 수학 B형 29번 기출문제 풀이 및 해설
[수능29번] 2015학년도 대학수능 수학 B형 29번 기출문제 풀이 및 해설
[수능29번] 2016년 10월 고3 학평(서울) 수학 가형 29번 기출문제 풀이 및 해설
[수능29번] 2015년 10월 고3 학평(서울) 수학 B형 29번, 30번 기출문제 풀이 및 해설
[인하대 수리논술] 2016학년도 인하대학교 논술우수자전형 자연계열(오후) 논술고사 기출문제
[서울대 심층구술면접] 2015학년도 서울대학교 수시 일반전형 심층구술면접 기출문제2
수선 PQ의 중점 M과 평행사변형의 대각선 CR의 중점이 일치하므로, 결국 이 빨간색 점 X는 앞 풀이에서와 일치합니다.
앞 풀이에서는 최적점인 빨간색 점 X의 좌표를 구하지 않고도 최댓값을 얻을 수 있었습니다만, 이 풀이에서는 점 X의 좌표를 일단 구해야지 싶습니다.
좋은 풀이가 못됩니다만, 끝까지 밀고 나가 보겠습니다.
먼저, 위치벡터 OR로부터 수선의 발 H'의 좌표를 구하면,
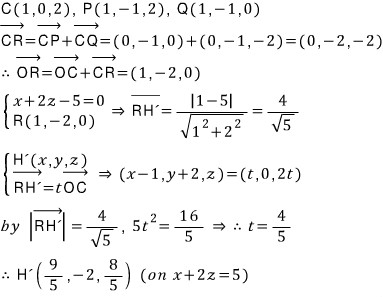
다음, 최적점 X의 좌표를 (x, y, z)로 두면 벡터 CX의 크기는 1이고 방향벡터가 벡터 H'C이므로 아래와 같이 최적점 X의 좌표를 구할 수 있습니다.
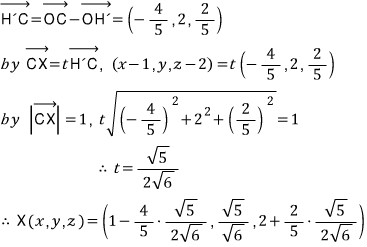
이제 마무리해 보면,
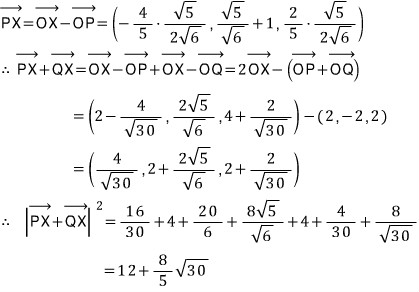
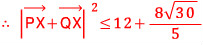
세 번째 풀이입니다.
점 P와 점 Q는 고정된 점이고 점 X는 중심이 C이고 반지름이 1인 원 위를 움직이는 점입니다.
벡터 PX와 QX의 합벡터의 기하적 의미를 따지기 보다는 두 벡터를 각각 원의 중심 C를 사용한 벡터들의 합으로 분해한 후 목표식을 정리해 보면,
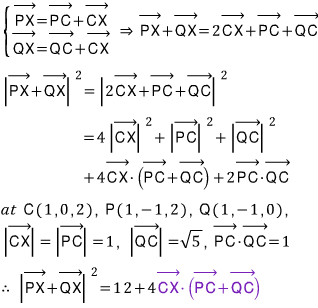
바로 앞 두 번째 풀이에서 벡터 CP와 CQ의 합벡터 CR과 벡터 CX가 이루는 각이 클수록 문제의 벡터 PX와 PQ의 합벡터의 크기는 최대가 된다고 하였습니다. 벡터 PC와 QC의 합벡터가 벡터 CR과 크기가 같고 반대 방향이므로, 벡터 PC와 QC의 합벡터가 벡터 CX와 이루는 각은 벡터 CR과 벡터 CX가 이루는 각의 보각이지요...
따라서 벡터 CR과 벡터 CX가 이루는 각의 크기가 클수록 이 보각은 작아지므로, 결국 위 보라색 내적의 크기가 클수록 목표식의 값이 최대가 되는 것과 같은 얘기가 되네요...
즉, 벡터 PC와 QC의 합벡터가 벡터 CX와 이루는 각의 크기를 θ 라 하면,
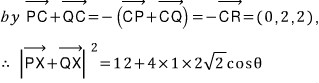
이고,
앞 풀이의 애니메이션에서 각 RCX의 크기가 최대가 될 때의 그 보각의 크기는 각 RCH'의 크기가 되므로,
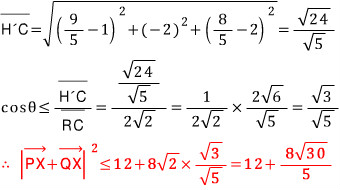
깔끔한 생각! 덧붙이기...
아래 애니메이션은 더 깔끔한 발상과 그에 따른 계산을 보여 주는 그림입니다.
실전 감각이 매우 뛰어난 경우입니다.
벡터 PC와 QC의 합벡터를 평행이동한 벡터가 위 그림에서 빨간색 벡터이고 그 위치벡터를 벡터 RC로 표현해 두었습니다.
파란색 벡터와 빨간색 벡터가 이루는 각의 크기, 또는 각 RCX의 크기가 최대가 되는 상황, 선분 RX의 길이가 최대가 되는 상황, 보각 관계, 여각 관계 등등을 한꺼번에 보여 주는 그림입니다.
벡터 CR의 종점을 가리키는 점 R의 좌표를 구한다든가, 수선의 발 H'의 좌표를 구한다든가, 선분 H'C의 길이를 구한다든가, 점과 평면 사이이의 거리 공식, 각종 피타고라스 등등등
이들 모든 수 연산은 더 이상 필요하지 않으며, 처음에 계산된 기본 좌푯값만을 가지고 내적 한 방으로 끝입니다.
다음은 네 번째 풀이입니다.
바로 앞 풀이에서와 마찬가지로 벡터 PX와 QX를 각각 원의 중심 C를 사용한 벡터들의 합으로 분해한 후 목표식을 정리하는 방향으로 출발...
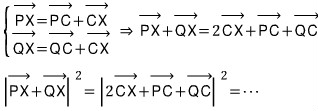
여기서 삼항 제곱식이 부담스럽습니다.
벡터 PC와 QC의 합... 벡터 CP와 CQ의 합... 에서 벡터 덧셈의 평행사변형의 법칙에서 평행사변형의 대각선의 교점을 생각합니다. 수선 PQ의 중점 M을 사용하여 위 식을 더 단순화해 봅니다.
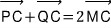
이므로,
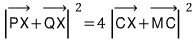
가 되네요... 벡터 MC와 CX의 합벡터가 첫 번째 풀이에 있는 벡터 MX입니다. 벡터 QX'의 절반...
어쨌든
처음 가진 발상과 풀이 방향에 따라 합벡터 MX에 대해 관심을 가지기 보다는 일단은 위 목표식을 전개해야 겠습니다.
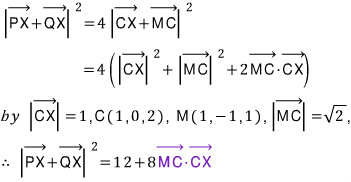
이 보라색 내적의 값은 세 번째 풀이에 있는 보라색 내적의 값의 절반입니다. 벡터 MC가 벡터 PC와 QC의 합벡터와 방향이 같고 크기만 절반이니까요...
어쨌든,
벡터 MC와 CX의 크기가 고정이므로 두 벡터가 이루는 각의 크기가 최소일 때 목표식의 값은 최대가 됩니다.
위 그림에서 계속하여,
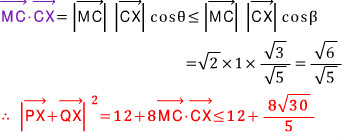
발상과 공간지각에 대하여,,,
벡터 OC가 단면원 C가 놓인 평면의 법선벡터이죠...
벡터 MC, 벡터 OC를 포함한 평면과 단면원 C가 놓인 평면의 교선이 문제 해결의 열쇠입니다. 이 교선 위에 최적점이 있을 것이라는 감각을 기를 수 있도록 많이 훈련해야 할 것입니다. 위에 링크한 게시글들은 이 힘을 기르기 위한 예제들이라고 생각할 수 있습니다.
진산서당 블로그 검색창에서 『평면 문제로 단순화』를 검색하셔도 됩니다...
단면원의 중심 C는 서로 다른 두 벡터 MC와 OC가 결정하는 평면 위의 점입니다. 동시에 단면원 C가 놓인 평면 위의 점이지요. 그런데 벡터 OC가 단면원 C가 놓인 평면과 수직인 법선벡터입니다. 그렇다면 점 C는 두 평면의 교선 위의 점입니다. 이때 두 벡터 MC와 OC가 결정하는 평면 위의 임의의 점을 지나 법선벡터 OC와 평행한 직선은 두 평면의 교선과 만나겠지요? 따라서 점 M에서 단면원 C가 놓인 평면에 내린 수선의 발 H는 두 평면의 교선 위의 점이 됩니다. 그리고 동시에 교선 HC는 원의 중심을 지나는 직선이므로 이 직선 위에 원 위의 점 X가 놓일 때 선분 HX의 길이는 최대가 되거나 최소가 되구요... 그리고 이때에 관련된 벡터들이 이루는 각의 크기 역시 최대 또는 최소 상황이 되는 것이지요...
늘 이런 식입니다.
다섯 번째 풀이입니다.
목표식이 벡터 PX와 QX의 합벡터의 크기에 관한 것입니다.
지금까지 우리는 삼각형의 법칙이나 평행사변형의 법칙 또는 그 평행이동을 통하여 벡터 PX와 QX의 합벡터가 기하적으로 무엇인지를 생각하거나, 단면원의 중심 C를 사용하여 두 벡터를 각각 분해하여 목표식을 정리한 연후에 그 기하적 의미를 살펴 보는 방향으로 풀이해 왔습니다.
처음부터 벡터 PX와 QX의 합벡터의 크기는 그 합벡터의 역벡터의 크기와 같다는 생각을 하면 좀 더 편합니다. 두 벡터의 시점이 일치하니까요... 즉,
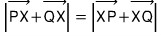
그 다음,
평행사변형의 대각선의 교점을 M이라 두면, 즉 수선 PQ의 중점을 M이라 두면 두 벡터의 크기의 합이 아래와 같이 바뀌므로 이제 벡터 MX의 크기가 최대가 되는 상황에 집중할 수 있게 되는 것이지요...
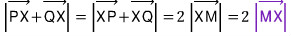
여기서,
벡터 MX를 단면원의 중심 C를 사용한 두 벡터의 합벡터로 분해하는 것이지요...
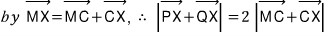
이 식의 양변을 제곱하고 우변을 정리하여 벡터 MC와 벡터 CX의 내적이 최대가 되는 상황으로 이끈 풀이가 바로 앞 네 번째 풀이가 되겠습니다.
우변을 제곱하여 내적으로 바꾸지 않고, 그냥 우변이 최대가 되는 상황을 살펴 보면,
삼각형 MCX에서 변 MC와 CX의 길이가 일정하므로 각 MCX의 크기가 최대가 될 때 변 MX의 길이가 최대가 되고 이때 목표식의 값이 최대가 되는 것이지요.
벡터 MC를 C방향으로 연장해서 생각해 보면, 각 MCX의 크기가 클수록 이 각의 보각은 작아지는데 이 보각이 바로 두 벡터 MC와 CX가 이루는 각이므로 이 각의 크기가 작아질수록 두 벡터 MC와 CX의 내적이 최대가 되는 상황이 됩니다.
결국 우변을 제곱하여 내적으로 문제를 해결하는 방식으로 연결됩니다.
직접적으로 변 MX의 길이의 최댓값을 구하는 방식을 고민해 봅니다.
이것이 바로 첫 번째 풀이에 있는 방식으로써, 점 M에서 단면원 C가 놓인 평면에 수선을 내려서(수선의 발 H), 직각삼각형 MHX의 빗변 HX의 길이가 최대가 되는 상황을 살피는 것이지요. 수선 MH의 길이가 일정하므로 변 HX의 길이가 최대일 때 빗변 MX의 길이가 최대가 되는데, 변 HX가 단면원의 중심 C를 지날 때 변 HX가 최대가 됨을 생각하면, 이제 피타고라스의 정리 등 연산으로 마무리할 수 있는 것이지요...
그런데,
첫 번째 풀이에서는 변 MH의 길이를 얻기 위해서 점과 평면 사이의 거리 공식을 사용하였고, 직각삼각형 MHC에서 피타고라스의 정리로 변 HC의 길이를 먼저 구하는 방식어어서 계산량이 많았습니다...
법선법터 OC를 최대한 활용하는 것이 좋습니다.
수선 MH가 법선벡터 OC와 평행하므로, 법선벡터 OC와 벡터 MC가 이루는 각의 크기를 α, 직각삼각형 MHC의 빗변 MC와 밑변 HC가 이루는 각의 크기를 β 라 하면, α + β = 90° 이므로,
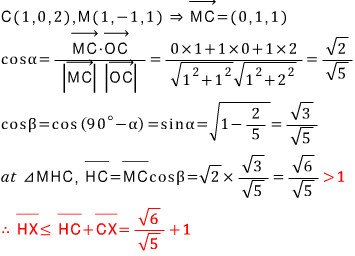
위 빨간색 부등호는 수선의 발 H가 단면원 C가 놓인 평면 위에서 원 C 바깥에 놓인 점임을 가리키고 있습니다.
마무리해보죠...
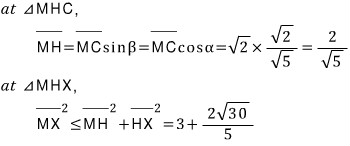
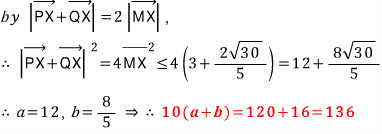
마지막 풀이입니다.
이상과 같이 기하적 접근으로 최적점을 찾는 방식이 아니라 좌표만을 이용해서 해결할 수 있는지를 생각해 보아야 겠습니다.
단면원 C 위를 움직이는 동점 X의 좌표를 (x, y, z)라 두고, 두 벡터 PX와 QX의 합벡터의 위치벡터를 성분 표시해보면,
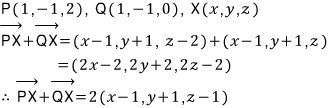
이므로, 목표식의 값은 아래와 같습니다.
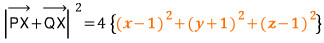
위 주황색 식이 가지는 의미가 무엇이죠?
네...
원 위의 점 (x, y, z)에 대하여 정점 (1, -1, 1)로부터 떨어진 거리의 제곱입니다.
정점 (1, -1, 1)이 바로 지금까지 살펴 본 수선 PQ의 중점 M이군요.
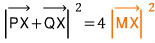
어쨌든,
정점 (1, -1, 1)에서 단면원 C가 놓인 평면에 수선을 내리면(수선의 발 H), 직각삼각형 MHX의 빗변 HX의 길이가 최대일 때 빗변 MX의 길이가 최대가 되므로,,,
이하 생략~~~
진산서당 (http://mathseodang.com) 허락하에 등록된 글입니다.