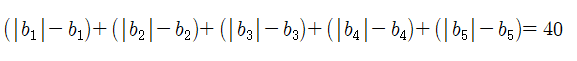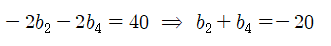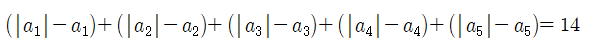등차수열과 등비수열에 관한 문제인데요. 문제에 의하면 각각의 첫째항과 공차, 공비가 모두 정수이기 때문에 모든 항은 정수임을 알 수 있겠습니다. 정수 조건은 문제 풀이에서 꽤 중요하므로 잘 기억해둔채 다음 생각을 이어가보겠습니다.
등차수열의 첫째항이 양수이고 공차가 음수라는 것은 어떤 성질이 있나요? 이런 조건이 나오는 문제 중 가장 흔한 문제가 "a₁이 얼마얼마이고 공차가 얼마얼마(음수)인데, 몇 번째항까지의 합이 최대인가?" 이런 문제죠. 이 문제의 답은 "항의 값이 양수인 마지막 항까지"임을 다들 알 것이라 생각합니다. 첫째항이 양수이고 음수인 공차를 갖는 등차수열은 특정 항까지는 모두 양수이다가, 바로 다음번째 항부터는 모두 음수인 형태를 가진다는 성질이 있습니다.
다음으로 등비수열의 첫째항이 양수이고 공비가 음수라면요? 공비가 음수이면 계속 양수, 음수, 양수, 음수, ... 가 번갈아 나타나므로, 이 등비수열의 홀수번째 항은 모두 양수, 짝수번째 항은 모두 음수임을 알 수 있습니다.

문제의 내용은 충분히 생각을 해보았으니 이제 박스 안의 내용을 살펴보겠습니다.
(가)에서는 수열 a의 1~5항, 수열 b의 1~5항을 모두 더한 값이 27이라고 합니다. 음.. 어쩌라는 건지 와닿는 부분은 없군요. 그냥 넘어가봅시다.
(나)는 수열 a의 항은 마찬가지로 1~5항을 더하고, 수열 b는 (가)와 달리 절댓값을 취하여 더한 값을 알려주고 있습니다. 느낌이 오나요? (가), (나) 식은 비슷한 항이 매우 많으므로 둘을 빼서 소거를 하면 좋은 결과가 나올 것 같습니다. 두 식을 변변 빼서 같은 번호의 항을 함께 묶어보면 다음과 같습니다.

b₁>0이므로 |b₁|=b₁이고, 둘을 빼면 0이군요. b₂<0이므로 |b₂|=-b₂라 둘을 뺀 값은 -2b₂입니다. 정리하면,

임을 알 수 있습니다.
이 정도 조건이면 첫째항, 공비가 정수임을 이용하여 충분히 수열 b를 구해볼 수가 있는데요. 공비를 r이라 하면, b₂(1+r²)=-20 이므로 1+r²은 20의 약수이고, 대입하여 찾아보면 음의 정수 r=-1, -2, -3이 가능합니다. 각 경우의 수열 b_n을 구하면

위와 같이 i), ii)의 두 가지의 가능성이 있음을 알 수 있습니다.

(가)와 (나)를 이용하여 수열 b를 구하고 나니 (다)에서는 무얼 해야할지 확실히 잘 보이는군요. (나), (다)의 변변을 빼면 좀전과 비슷한 형태로 수열 a에 관한 식을 얻을 수 있습니다.

a₁>0이므로 |a₁|-a₁=0입니다. 이번엔 어느 항이 음수인지를 미리 알 수 없는 관계로 각각의 경우를 나누어보아야 합니다. 다만, 처음에 언급한 등차수열의 성질에 의해 k번째 항까지는 값이 양수이고, k+1번째 항부터는 값이 음수인 k가 반드시 존재할 것입니다. 일어날 수 있는 경우를 나누어 살펴보면 다음과 같습니다.

ㄴ)부터 하나씩 봅시다. ㄴ)에서는 a₅=-7인데 a₄≥0이려면 공차가 -7이하여야 합니다. 역으로 7씩 더하여 1~3항을 확인해보면 a₃≥7, a₂≥14, a₁≥21로, 1~5항의 합은 35이상의 어떤 자연수 값이 됩니다.
ㄷ)에서는 각 항이 정수임을 고려하면, ① a₄=-2, a₅=-5이거나 ② a₄=-1, a₅=-6 둘 중 하나입니다. (a₄=-3, a₅=-4일 때는 a₃도 음수라 조건에 맞지 않습니다.)
①의 경우에는 a의 각 항은 첫항부터 7, 4, 1, -2, -5이고, ②의 경우에 각 항은 14, 9, 4, -1, -6이 됩니다.
ㄹ)에서 a₃ + a₄ + a₅ 의 값은 3a₄ 와 같으므로, 각 항이 정수가 될 수 없습니다. 조건에 맞지 않고요, ㅁ)에서도 모든 항이 정수임이 불가능 하므로 역시 조건에 맞지 않습니다.

이렇게 수열 a와 수열 b의 1~5항이 각각 몇 가지 경우들이 나왔는데요. 어떤 경우가 맞을까요? 변변 빼서 얻은 조건만으로 여기까지 얻었으므로 이제 (가), (나), (다) 중 어느 한 식에 직접 넣어보면 확인이 가능합니다. 가장 간단한 (가)에 넣어봅시다.
(가)에 의하면 수열 a의 1~5항까지와 수열 b의 1~5항까지를 모두 더한 값이 27입니다.
한편, 수열 a의 1~5항의 합은 ㄴ)의 경우 35이상, ㄷ)①의 경우 5, ㄷ)②의 경우 20이고, 수열 b의 1~5항의 합은 i)의 경우 10, ii)의 경우 22입니다.
따라서, 합이 27이 될 수 있는 경우는 수열 a의 합이 5이고, 수열 b의 합이 22인 경우가 유일합니다.

수열 a는 순서대로 7, 4, 1, ... 인 등차수열이므로 제7항의 값은 -11, 수열 b는 순서대로 2, -4, 8, ... 인 등비수열이므로 제7항은 128이고 그 합은 117입니다. 

수학의 정도(正道) - 대홍쌤 블로그의 허락을 받아 올리는 해설입니다.