2017년 10월 교육청 가형 21번 [진산서당]

계속하여,,,

그저께 2017년 10월 17일 화요일 시행된, 

서울교육청이 주관한 고3 전국연합학력평가 수학 가형 21번 기출문제에 대한 풀이 및 해설입니다.

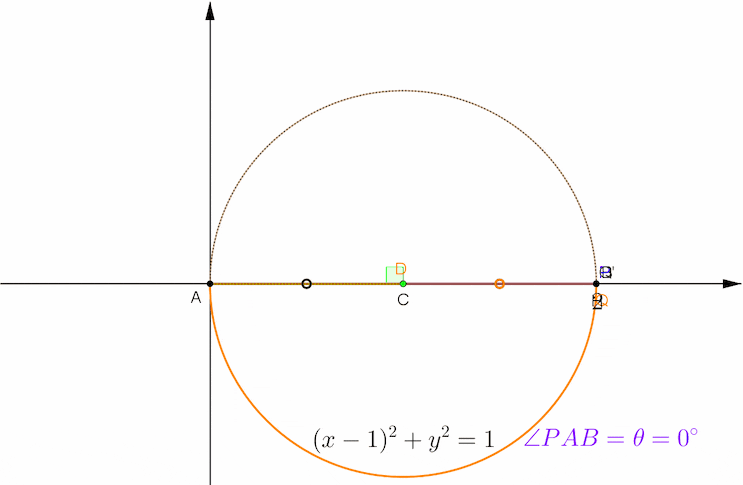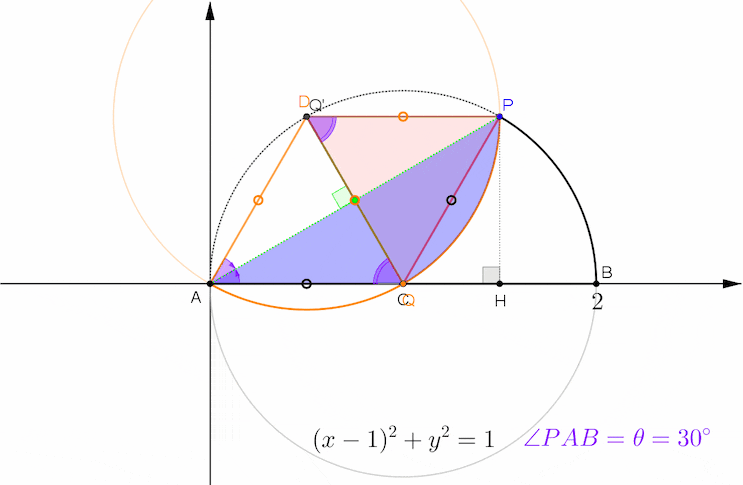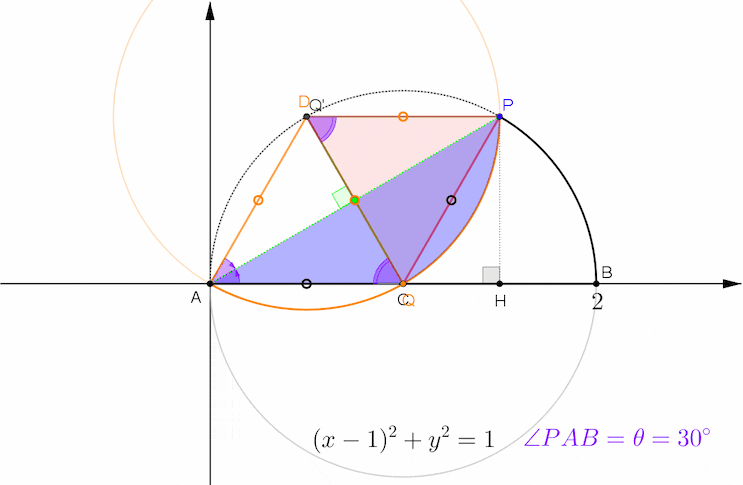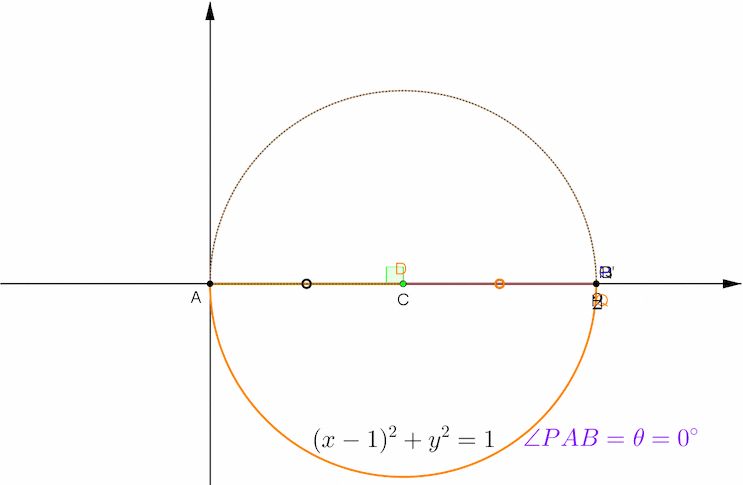
아래 애니메이션에서 초록색이 현 PA를 접는 선으로 해서 접었을 때의 대칭관계를 보여 주고 있습니다. 검은색 원과 주황색 원의 중심 C, D를 연결한 선분이 공통현 PA의 수직이등분선이고, 두 원의 반지름이 1로 같으므로 사각형 ACPD는 마름모가 됩니다.

초록색 공통현 PA, 주황색 원호 PQ, 반원의 지름 AB의 일부인 선분 AQ로 둘러싸인 파란색 영역이 포개어 지는 부분이고 이 영역의 넓이가 S(θ) 입니다.

가운데에 Ο로 표시된 선분들이 길이가 1인 반지름들이며, 보라색 작은 각 PAC, PAD의 크기가 θ 입니다. 따라서 빨간색 삼각형 DPQ는 꼭지각 D의 크기가 2θ 인 이등변삼각형이고, 삼각형 DAQ는 밑각의 크기가 2θ 인 이등변삼각형입니다.

이밖에도 여러가지를 관찰할 수 있습니다.

초록색 공통현 PA의 길이는 2cosθ 이고, 두 중심 사이의 거리인 초록색 선분 CD의 길이는 2sinθ 이며, 

주황색 원호 PQ에 대한 원주각 A와 검은색 원호 PB에 대한 원주각 A의 크기가 θ 로 같으므로 이들 호의 길이는 같으며, 그 길이는 2θ 이고, 호 PQ와 대칭인 호 PQ'의 길이도 마찬가지이지요...

공통현 PA와 호 PA로 이루어진 검은색 원의 활꼴과 주황색 원의 활꼴이 합동이며, 또 주황색 현 AQ, 호 AQ로 이루어진 활꼴과 대칭인 활꼴은 검은색 현 AQ', 호 AQ'로 이루어진 활꼴이고, 주황색 현 PQ, 호 PQ로 이루어진 활꼴과 대칭인 활꼴은 검은색 현 PQ', 호 PQ'로 이루어진 활꼴입니다.

이제,

파란색 영역의 넓이 S(θ) 를 θ 에 관한 식으로 나타낼 차례...

방법은 여러가지이겠네요...

삼각형의 넓이 공식, 부채꼴의 넓이 공식, 활꼴의 넓이 구하는 요령 등등에 대하여 자유로와야 겠습니다.

공식들을 한 번 쭈욱 적어 보죠...

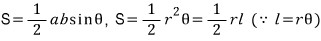
아래는 파란색 영역의 넓이를 큰 활꼴(PQA, PQ'A)에서 작은 활꼴(QA, Q'A)의 넓이를 빼주는 방식으로 구한 것입니다.

여기서, 활꼴의 넓이는 부채꼴의 넓이에서 이등변삼각형의 넓이를 빼주면 되겠는데,

큰 활꼴에 대응하는 부채꼴의 중심각 PCA, PDA의 크기는 π - 2θ 이고, 작은 활꼴에 대응하는 부채꼴의 중심각 QDA, Q'CA의 크기는 π - 4θ 이므로,

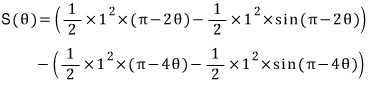
가 됩니다.

묻고 있는 것이 S(θ) 가 최대가 되게 하는 각 θ 에 대하여 cos2θ 의 값입니다.

위 식을 정리하여 미분으로 마무리해야 겠습니다. 기하적으로는 직관이 안되는 문제이다 싶습니다.

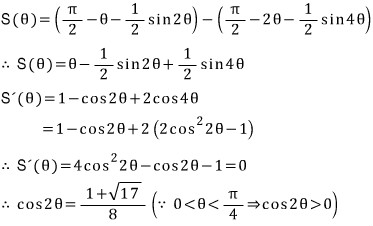
cos2θ 에 관한 이차방정식의 해가 하나는 음수이고 다른 하나는 양수인데, 주어진 θ 의 범위를 만족하는 해는 양수여야 하고,

따라서 정답은 오지선다형 ④ 번이겠는데,,,

여기서,

극대, 극소 판정이 조금 헷갈리는데,,, 꼭 챙기시기를 바랍니다.

아래로 볼록인 이차함수의 그래프를 생각하면, 큰 근 좌우에서 이차함수의 부호가 음에서 양으로 바뀌므로 즉, S'(θ) 의 부호가 음에서 양으로 바뀌므로 극소가 아니냐는 것인데요,,,

이 구간에서 코사인 함수가 감소임을 고려하면, S'(θ) = 0 을 만족하는 θ 값 좌우에서 S'(θ) 의 부호는 양에서 음으로 바뀌므로 극대가 됩니다...

이해되십니까???

합성함수나 치환한 경우에,

중간에 감소함수가 끼이는 경우는 반드시 조심을 해야하는 부분입니다.

아래 그래프는 참조용입니다.

위 그림에서 θ = α 일 때 S'(θ) = 0 이고,

θ = α 의 좌우에서 y =  cos2θ 는 감소하고 있습니다. 그렇다면, 이때 검은색 포물선의 x (x = cos2θ) 가 감소하게 되므로 빨간색 큰 점 (1+√17 / 8, 0) 의 오른쪽에서 왼쪽으로 가면서 이차함수 y 의 부호 즉, S'(θ) 의 부호는 양에서 음으로 바뀌고 있습니다.

결국, θ = α 의 좌우에서 S'(θ) 의 부호는 양에서 음으로 바뀌므로 극대...

다른 풀이에 대한 생각입니다.

삼각형 DAQ가 밑각의 크기가 2θ 인 이등변삼각형이므로 점 Q의 x 좌푯값은 2cos2θ 이고,

직각삼각형 PAH에서 빗변 PA의 길이가 2cosθ 이므로 점 P의 x 좌푯값은 2cosθcosθ 가 됩니다.

그런데, 주황색 원의 방정식을 얻는 것이 불편할 뿐만아니라 설사 얻더라도 식이 복잡하므로 정적분으로 파란색 영역의 넓이 함수 S(θ) 를 구하려고 시도하는 것은 최악입니다...

대신에,

삼각형 PAQ의 넓이에 현 PQ와 호 PQ로 이루어진 활꼴의 넓이를 더하는 방식으로 넓이 함수 S(θ) 를 구해 보겠습니다.

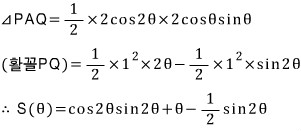
사인 배각 공식을 적용하면 앞 풀이에서 구한 S(θ) 와 같음을 알 수 있구요...

이 상태로 그냥 곧장 미분하거나, sin2θ 로 묶어서 곱의 미분법을 적용할 수 있겠는데, 앞 풀이와 대동소이합니다.

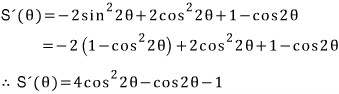
그런데,

곧장 미분하지 않고 배각 공식을 먼저 적용하여 S(θ) 를 깔끔하게 얻어 보려는 시도는???

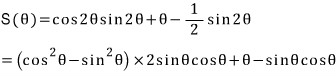
여기서 더 이상의 정리를 관두고 멈춰야 겠습니다.

이 상태로 굳이 미분하려고 덤비느니 앞 풀이가 훨씬 낫지요...

2θ 가 아니라 θ 에 관한 식으로 나타내고자 해도 미분한 식인 S'(θ) 에 배각 공식을 적용하는 것이 낫겠고요...

또 굳이 cosθ 의 4차식으로 끌고 갈 필요도 없습니다.

묻고 있는 것이 S(θ) 가 최대가 될 때의 cos2θ 의 값이지요...

이 문제는...

① 도형 지식, 도형 관계를 다루는 힘!

② 삼각함수식의 계산력과 미분 타이밍

③ 묻고 있는 것과 주어진 상황에 능동적으로 대처해서 타개해 나가는 여러가지 솜씨

등을 종합적으로 다루고 있습니다.

넘이 풀어 놓은 최종 답안만 열심히 본다고 이런 힘이 길러 지는 것이 아님을 꼭 유념하셔야 겠습니다.

혼자 힘으로 실전처럼!

(오답률 53%)

진산서당 블로그의 허락을 받아 올리는 해설입니다.