2018년도 6월 평가원 나형 30번 [진산서당]

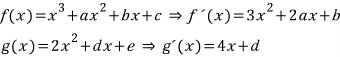
단순히 위와 같이 놓고, 조건 (가), (나)를 적용하여 정리한 후, 목표식과 엮는 방향으로 밀고 나갈 수 있습니다.

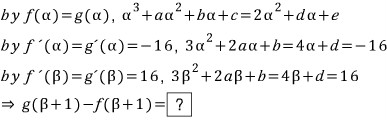
흠~~~ 너무 피곤하겠고요ㅜㅜㅜ

조건 (가), (나)를 아래와 같이 달리 적어 봅니다.

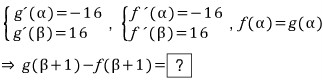
이차함수 g(x) 가 선대칭 도형인 포물선임을 생각하면 축의 방정식은 x = (α + β) / 2 가 되므로

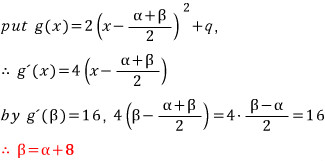
다른 한편으로 곰곰히 생각해 보면, 평행이동에 의하여 두 그래프의 모양이 바뀌지 않을 뿐만 아니라 목표식의 값도 달라 지지 않습니다.

그렇다면 최고차항의 계수가 2인 이차함수 g(x) 를 g(x) = 2x^2 으로 둘 수 있고,

이때, g'(x) = 4x = ±16 에서 α = -4, β = 4 가 됩니다. 그리고 이때, f(α) = g(α) = g(-4) = 32 가 되고요...

그리고 또 이때, 최고차항의 계수가 1인 삼차함수 f(x) 도 아래와 같이 확정할 수 있습니다.

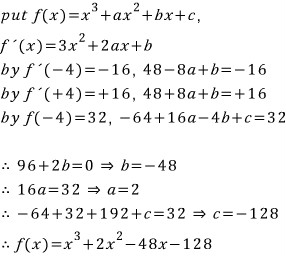
마무리하면,

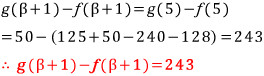
(오답률 1위 95%)

아래 애니메이션은 해설 참조용입니다.

주황색이 평행이동한 후에 문제의 조건에 맞게 그린 것이고, 움직이고 있는 파란색은 일반적인 f(x) 와 g(x) 의 그래프를 문제의 조건에 맞게 그린 것입니다. 단, x 축과 y 축 상의 눈금의 길이 비는 1:10.

빨간색 선분의 길이가 늘 일정함을 알 수 있지요...

다른 풀이입니다.

오답률이 95%로 높은 것을 보면, 많은 학생들이 평행이동을 이용하면 간단히 해결될 것이라는 발상을 못했다 싶네요...

조건 (가)에서 x = α 일 때 f(x) 와 g(x) 의 함숫값도 같고 미분계수도 같으므로, 함수식 f(x) - g(x) 는 (x - α)^2 을 인수로 가지며, f(x) 가 최고차 항의 계수가 1인 삼차함수이고 g(x) 가 이차함수이므로,

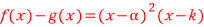
와 같이 둘 수 있고,

양변을 미분하면

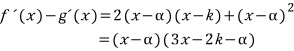
인데,

조건 (나)에서 f '(β) - g'(β) 라 하였고, α, β 에서 미분계수가 다름을 생각하면, f '(β) - g'(β) = 0, α ≠ β 이므로

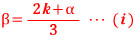
의 관계가 성립합니다.

그리고, 앞선 풀이에서 미분계수 ±16을 최고차항의 계수가 2인 이차함수 g(x) 에 적용하여 아래 관계를 얻었고요...

또, 빨간색 삼차함수식 f(x) - g(x) 에 의하여 목표식은 아래와 같습니다.

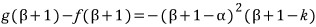
먼저, 식 (i) 을 적용하여 k 를 소거해 보아야 겠는데,,,

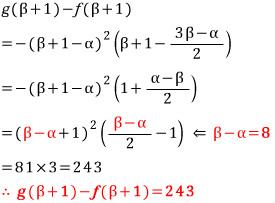
도중에 β - α 가 식 (ii) 에 의하여 8임을 적용할 수 있어서 정답을 얻을 수 있게 됩니다.

이상의 풀이는 EBS 해설에서 힌트를 얻어서 재구성한 것인데요,,,

f(α) = g(α),

f '(α) = g'(α)

f '(β) = g'(β)

이 세 조건으로부터, 새로운 삼차함수 f(x) - g(x) 를 설정하고 그 미분으로 헤쳐 나가 보자는 발상입니다.

좋네요...

그리고, 식 (ii) 는 이차함수에서 미분계수의 부호가 반대로 주어졌으므로 대칭성으로 엮어낸 것인데, 이는 자연스럽고요...

이상입니다.

진산서당 블로그(http://mathseodang.com/) 허락을 얻어 올리는 해설입니다.