2019년도 6월 평가원 가형 21번 [진산서당]
함수 f(x) 의 그래프, 이로부터 모든 실수 t 에 대하여 정의된 함수 g(t) 의 그래프를 얻는데까지가 1단계이겠고, 그 다음에 사차함수 h(x) 와 물려 있는 합성함수 h ο g 를 살펴 보는 2단계로 나누어서 헤쳐 나가야 겠습니다.
먼저, 함수 f(x) 의 그래프...
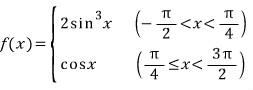
cos(π/4) = √2/2 = sin(π/4) 이지요. sin(π/4)를 세제곱하면 2√2 / 8 이고 이를 두 배하면 √2/2 로써, 결국 x = π / 4 에서 연속입니다. - π / 2 < x < π / 4 범위에서 sinx 가 -1에서 원점 O를 지나 √2/2 까지 증가해 가는 그 모양과 비슷하게 2sin^3(x) 는 -2에서 원점 O를 지나 √2/2 까지 증가해 갑니다. π / 4 < x < 3π / 2 범위에서 cosx 는 √2/2 → 0 → -1 → 0 인 코사인 파형 그대로이고요...
아래 애니메이션에서 검은색이 열린 구간 (- π/2, π/4) 에서 정의된 함수 y = f(x) 의 그래프입니다.
그 다음, 파란색이 f(x) - t 의 그래프...
함수 f(x) 의 최댓값이 √2/2 이므로 f(x) 에서 √2/2 이상인 t 값을 빼면 파란색 f(x) - t 의 그래프는 항상 0이하이고, 여기서 절댓값을 취하여 x 축에 대칭되도록 꺾어 올린 것이 보라색 |f(x) - t|의 그래프입니다. 이 정도까지는 그릴 수 있어야 겠고요... 여기서 근호를 취한 것이 주황색 √|f(x) - t|의 그래프인데, 실전에서 이 정도까지 완전하게 그리는 것은 불가능할 뿐만아니라 그럴 필요도 없다 싶고요,,, 개형을 어느 정도만 상상하거나 크리티컬한 부분만 따로 확인해 낼 수 있으면 충분합니다.
아래 애니메이션에서 파란색으로 바뀌고 있는 수식 부분요...
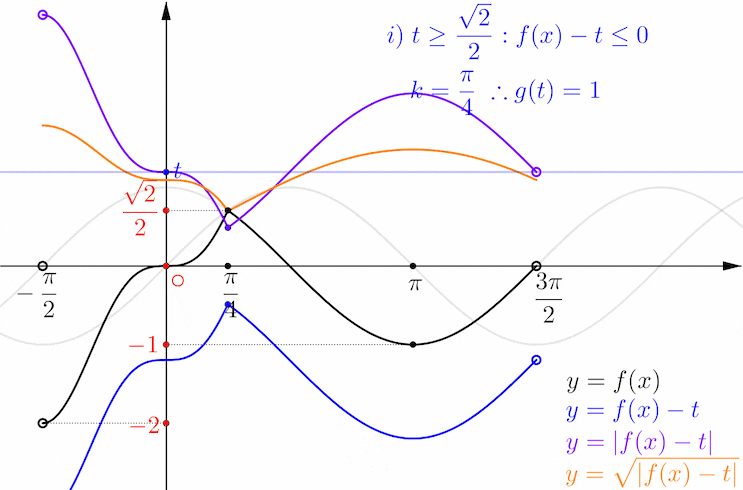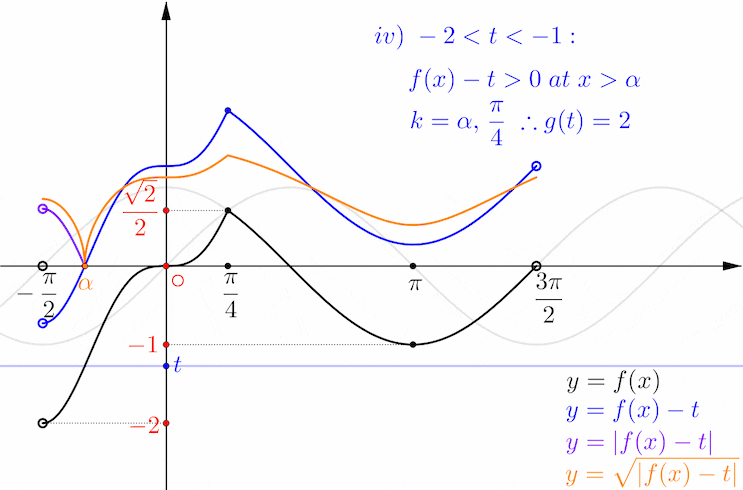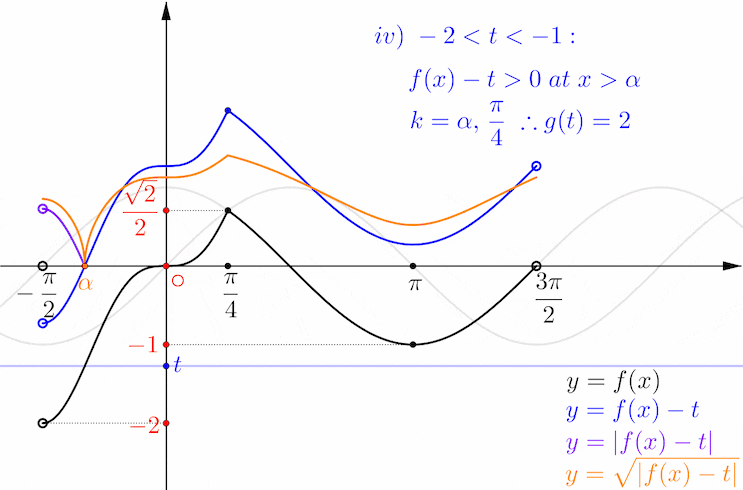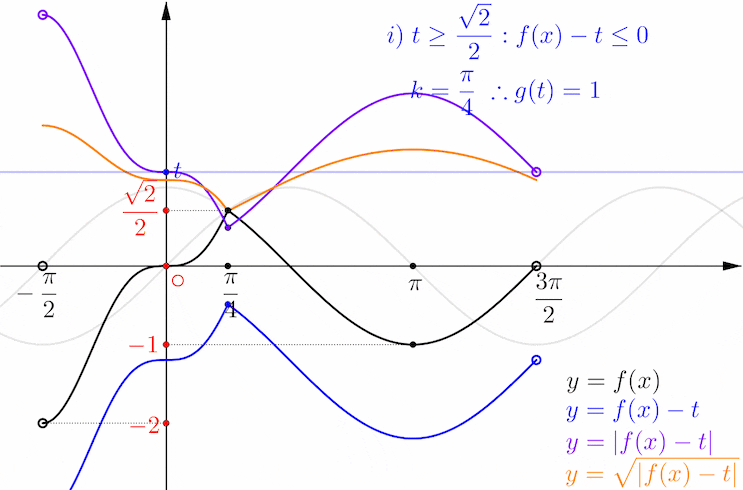
i) 번이 t ≥ √2/2 일 때이고, 열린 구간 (- π/2, π/4) 에 속하는 실수 k 중에서 주황색 함수가 미분이 불가능한 k 값은 k = π/4 하나 뿐입니다. 따라서 이 범위의 실수 t 에 대하여 g(t) = 1 이 되겠습니다.
불필요한 확인일 수도 있겠지만,,,
열린 구간 (- π/2, π/4) 에서 함수 f(x) 의 미분불가능성은 x = π / 4 를 확인하는 것으로 충분합니다.
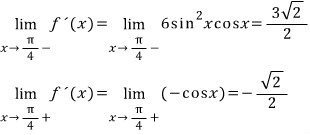
그리고,
열린 구간 (- π/2, π/4) 에서 주황색 함수 √|f(x) - t|가 미분 불가능한 k 값은 아래에서 보듯이 보라색 함수가 미분 불가능한 점 또는 x 축과 만나는 점의 x 값이 되고 있음을 알 수 있습니다.
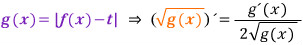
참고로,,,
아래 애니메이션에서 파란색 함수 f(x) - t 가 양수일 때는 굳이 보라색으로 칠하지 않고 그대로 파란색으로 두었으며, x 축에 대칭이 되어 꺾여 올라온 부분만 보라색으로 표시하였습니다.
다음,,, ii) 0 < t < √2/2 일 때
파란색 함수 f(x) - t 는 x = α 와 x = β 두 곳에서 x 축과 만나며 α < x < β 구간에서만 f(x) - t 양수입니다. 파란색 함수 f(x) - t 의 음수 부분이 x = α 와 x = β 에서 꺾여서 위로 올라온 부분을 보라색으로 표시했습니다.
x = α, π/4, β 세 곳에서 미분 불가능이므로 이 범위에서 g(t) = 3
다음,,, iii) -1 < t < 0 일 때
실수 t 의 값이 i), ii) 를 거쳐 점차 작아 지면 파란색 함수 f(x) - t 의 그래프는 점차 위로 올라가는데, 이 범위에서 파란색 함수 cosx - t 가 x 축과 만나는 점이 하나 더 늘어납니다. x > γ 구간도 x 축 위로 올라 가는 것임.
x = α, π/4, β, γ 네 곳에서 미분 불가능이므로 이 범위에서 g(t) = 4
다음,,, iv) -2 < t < -1 일 때
파란색 코사인 파형이 이제 완전히 x 축 위로 올라 가고 파란색 함수 f(x) - t 가 음수인 구간은 x < α 뿐입니다.
x = α, π/4 두 곳에서 미분 불가능이므로 이 범위에서 g(t) = 2
다음,,, v) t ≤ -2 일 때
열린 구간 (- π/2, π/4) 에서 파란색 함수 f(x) - t 의 그래프 전체가 x 축 위로 올라 갔습니다.
x = π/4 에서만 미분 불가능이므로 이 범위에서 g(t) = 1
위 애니메이션을 보고 있자니 많이 헷갈리는데요,,, 그냥 위에서 나눈 구간별로 파란색과 보라색 그래프를 그려 보면 별거 없습니다.
t = 0, t = -1 일 때를 따져 보지 않았는데요...
이 두 부분이 사실 가장 어렵습니다.
t = 0 이면 파란색이 검은색과 일치할 때입니다. x = π/4 와 x = β(π/2) 에서는 명백히 미분불가능이고 x = γ(3π/2) 는 범위 밖입니다. x = α(0) 만 따져 주면 되겠는데, 위 검은색 그래프에서 x < α(0) 부분인 아랫쪽을 접어 올린다고 했을 때 x = α(0) 에서 미분계수는 그대로 0이지 싶은데, 주황색 그래프의 경우는 그렇지 않아 보이네요...
식으로 확인해 보겠습니다.
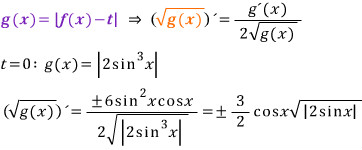
일견 x = α(0) 에서 분모가 0이므로 미분 불가능으로 보이지만 분자의 차수가 높음을 생각하면 x → α(0) 에서 미분계수가 0임을 알 수 있습니다.
미분계수의 정의로 살펴 보겠습니다.
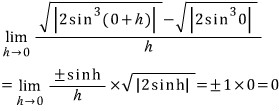
따라서 t = 0 일 때 x = π/4, β(π/2) 에서만 미분불가능이므로 g(t) = 2
t = -1 이면 β = γ = π 에서 파란색 함수 f(x) - t = cosx - t 가 x 축에 접할 때인데, 파란색은 당연히 미분계수가 0인데, 주황색 함수는 어떻게 될지???
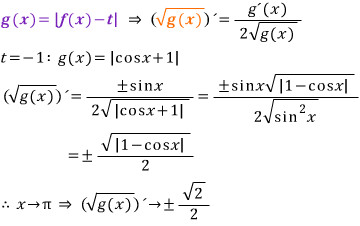
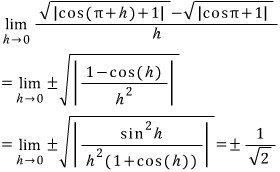
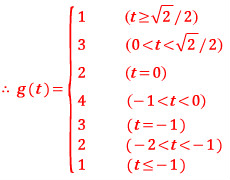
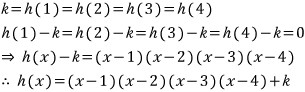
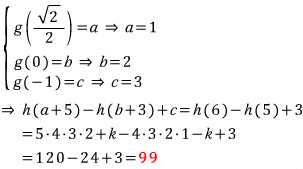
이상입니다.
진산서당 블로그(http://mathseodang.com/) 허락을 받아 올리는 해설입니다.
|
|
|